Stochastic gradient Hamiltonian Monte Carlo

Recently I came across this paper on Hamiltonian Monte Carlo with stochastic gradients. Since it is very relevant to my research, I thought I will have a look. Here are my thoughts and comments on the paper.

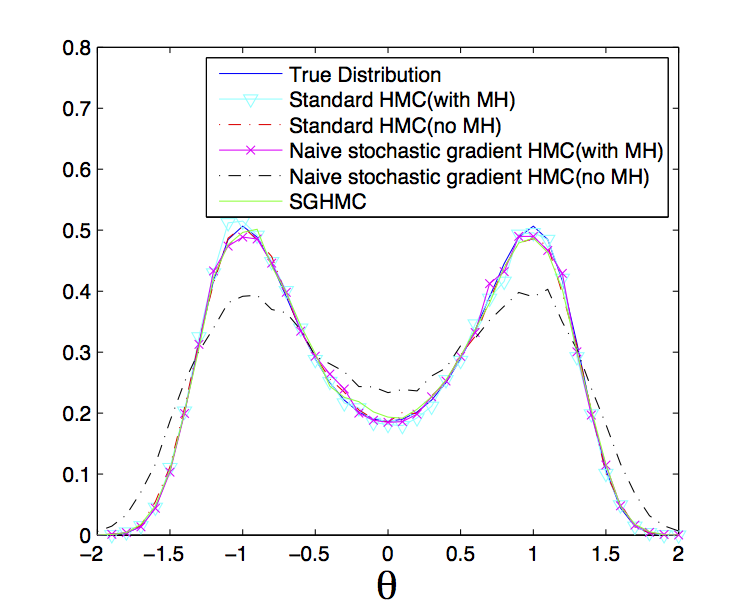
Hamiltonian Monte Carlo(HMC) is one of my research areas. One of the most annoying thing about the HMC is that gradients of the probability distribution is required for the sampling. A MATLAB code is available in [GitHub](https://github.com/tqchen/ML-SGHMC. Below is a plot from this paper which compare the true input distribution with the one recovered by HMC.

The MATLAB code is simple to understand. See the gist below

function [ newx ] = sghmc( U, gradU, m, dt, nstep, x, C, V )
%% SGHMC using gradU, for nstep, starting at position x

p = randn( size(x) ) * sqrt( m );
B = 0.5 * V * dt;
D = sqrt( 2 * (C-B) * dt );

for i = 1 : nstep
    p = p - gradU( x ) * dt  - p * C * dt  + randn(1)*D;
    x = x + p./m * dt;
end
newx = x;
end

What I would like to see is its application to large-scale problems. My concern is that the choice of parameters, for example the friction B,

can have huge effect on the performance of the sampler.