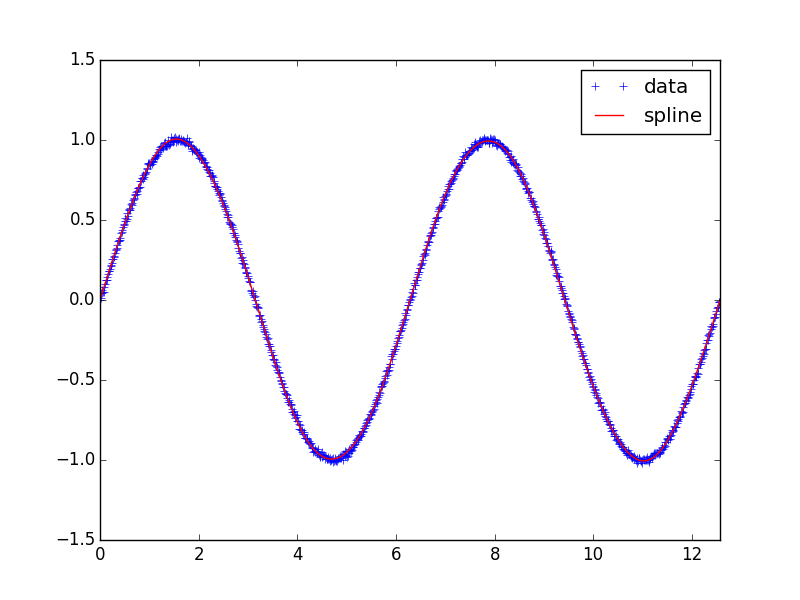
Splines are extremely useful to represent data when the underlying model is unknown or expensive to compute. I use them as a part of my cosmological calculations. In this post I explore the publicly available codes for computing splines. Here is an example of a noisy sine curve in [0,4pi] and smoothed spline curve obtained with GSL B-splines.
Gnu Scientific Library (GSL)
GSL offer B-splines as a part of the library. In c/c++ we can use the functionality by
#include <gsl/gsl_bspline.h>An example program can be found here
Eigen library
Eigen is known for its excellence in linear algebra. It also offers a large set of unsupported modules. Splines is one of them. Below you can find a simple code I found in KDE forum
#include <unsupported/Eigen/Splines>
typedef Spline<double,2> Spline2d;
typedef Spline2d::PointType PointType;
typedef Spline2d::KnotVectorType KnotVectorType;
typedef Spline2d::ControlPointVectorType ControlPointVectorType;
ControlPointVectorType points = ControlPointVectorType::Random(2,100);
const Spline2d spline = SplineFitting<Spline2d>::Interpolate(points,3);
KnotVectorType chord_lengths; // knot parameters
Eigen::ChordLengths(points, chord_lengths);
for (Eigen::DenseIndex i=0; i<points.cols(); ++i)
{
PointType pt = spline( chord_lengths(i) );
PointType ref = points.col(i);
VERIFY( (pt - ref).matrix().norm() < 1e-14 );
}Einspline library
Einspline library offers excellent spline fitting facilities. There are several bases available, for example, linear, logarithmic and general. The code is written in c and runs fast. We can get the 1-D splines by including
#include <nubspline.h>Benchmarking splines
I needed to see how each of these libraries compare to each other and decided to code up a benchmarking repository in github. It can be found here
