Markov Chain Monte Carlo is an excellent tool for estimating posterior densities. The output of these algorithms are samples from the posterior probability distribution of parameters. One can easily obtain summary statistics from these samples, for example mean and standard deviation. However if the posterior distribution is used as an input to another Bayesian problem, we need a method of estimating the probability given a random sample from the posterior space. This is where the KDE is extremely useful.
Overview
In Python, R and MATLAB there are plenty of off-the-shelf libraries available for posteriors with reasonably large dimensions. However, it is hard to find a stable library in c, c++ and fortran. I was looking at github and found the following open source codes.
- https://github.com/timnugent/kernel-density
- https://github.com/KaiyuanWu/fastKernelDensityEstimation
- https://github.com/jmarshallnz/adsmooth.git
- https://github.com/vmorariu/figtree.git
Every one of these have interesting aspects but none of the matched the requirements of my problem. My requirements where
- a header only library
- can handle large dimensions
- fast
- efficient memory management
Since none of the codes satisfied all 4 requirements, I started my own version of it. You can find the code in GitHub. My idea is that the kernels can be specified as a template parameter. Then we can create an efficient library with many different kernels. A demo code is shown below
#include <KernelDensityEstimation>
template<typename realScalarType>
void GaussAllNbs(std::vector< std::vector<realScalarType> > const & dataIn)
{
typedef kde::Gaussian<realScalarType> kernelType;
typedef kde::DiagonalBandwidthMatrix<realScalarType> bandwidthType;
typedef kde::AllNeighbours<realScalarType> neighboursType;
typedef kde::KernelDensityEstimator<kernelType,bandwidthType,neighboursType> kdeType;
typedef typename kdeType::realVectorType realVectorType;
typedef typename kdeType::realMatrixType realMatrixType;
typedef typename kdeType::indexType indexType;
assert(dataIn[0].size() == 3);//will work for a 2-d pdf only!
realMatrixType samples(dataIn.size()/4,dataIn[0].size()-1);
for(size_t i = 0; i<dataIn.size()/4; ++i)
{
for(size_t j=0; j<dataIn[0].size()-1; ++j)
{
samples(i,j) = dataIn[i][j];
}
}
// build kde
kdeType kde(samples);
// find the bounds of the 2-d pdf
const realScalarType xMin = samples.col(0).minCoeff();
const realScalarType xMax = samples.col(0).maxCoeff();
const realScalarType yMin = samples.col(1).minCoeff();
const realScalarType yMax = samples.col(1).maxCoeff();
// create a plottable data
const indexType numSteps = 100;
const realScalarType dx = (xMax - xMin)/(realScalarType) numSteps;
const realScalarType dy = (yMax - yMin)/(realScalarType) numSteps;
std::ofstream outFile;
outFile.open("plot-bi-variate-Gauss.dat",std::ios::trunc);
outFile<<std::scientific;
for(indexType i=0;i<numSteps;++i)
{
realScalarType xi = xMin + i*dx;
for(indexType j=0;j<numSteps;++j)
{
realScalarType yi = yMin + j*dy;
realVectorType samp(2);
samp(0) = xi;
samp(1) = yi;
//outFile<<std::setprecision(10)<<xi<<","<<yi<<","<<kde.compute(samp)<<std::endl;
outFile<<std::setprecision(10)<<xi<<","<<yi<<","<<kde.computePDF(samp)<<std::endl;
}
outFile<<std::endl;
}
outFile.close();
}
int main()
{
typedef double realScalarType;
std::string fileName("../data/bi-variate-Gauss.dat");
std::vector< std::vector<realScalarType> > dataIn;
utils::readData<realScalarType>(fileName,',',dataIn);
GaussAllNbs<realScalarType>(dataIn);
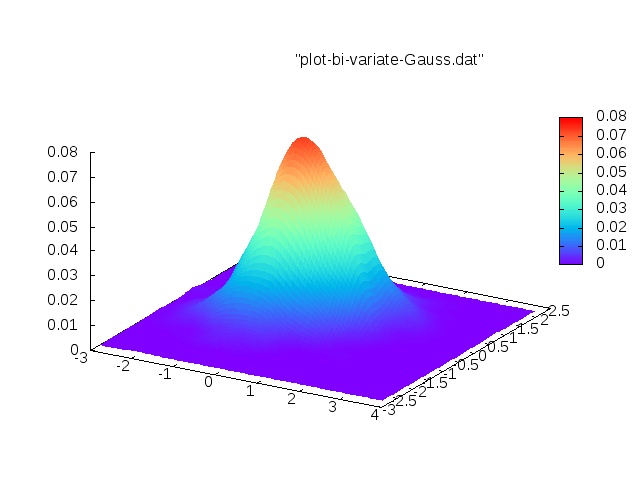
}Here is an example of a 2-D density I recreated with my code