Last week I bought an Intel Xeon Phi off EBay. My plan is to create a desktop supercomputer! This is an extremely challenging but exciting project.
The excitement
One of my areas of my research is spherical harmonics (used in power spectrum estimation of cosmological data) and two of the codes that are available for fast Spherical Harmonic Transform (SHT) is parallelized by OpenMP. I believe Xeon Phi is ideal for this computation. People in Caltech did a performance analysis a few years ago on Xeon Phi and their paper gives a good insight. They do caution about what can be achieved.
While most heritage software will run on the Xeon Phi with little effort, there’s no guarantee it will run optimally to fully exploit its architecture, even if the segments that carry out intensive numerical computations have been highly parallelized.
I found a sample code in their paper which shows how “easy” it is to offload the highly parallelizable parts of the code to Xeon Phi. Take a look below
#ifndef MIC_DEV
#define MIC_DEV 0
#endif
#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
#include <mkl.h> /* needed for the dsecnd() timing function. */
#include <math.h>
/* Program test1.c: multiply two matrices using explicit looping of elements. */
/*---------------------------------------------------------------------*/
/* Simple "naive" method to multiply two square matrices A and B
to generate matrix C. */
void myMult(int size,
float (* restrict A)[size],
float (* restrict B)[size],
float (* restrict C)[size])
{
#pragma offload target(mic:MIC_DEV) in(A:length(size*size)) \
in( B:length(size*size)) \
out(C:length(size*size))
{
/* Initialize the C matrix with zeroes. */
#pragma omp parallel for default(none) shared(C,size)
for(int i = 0; i < size; ++i)
for(int j = 0; j < size; ++j)
C[i][j] = 0.f;
/* Compute matrix multiplication. */
#pragma omp parallel for default(none) shared(A,B,C,size)
for(int i = 0; i < size; ++i)
for(int k = 0; k < size; ++k)
for(int j = 0; j < size; ++j)
C[i][j] += A[i][k] * B[k][j];
}
}
/*---------------------------------------------------------------------*/
/* Read input parameters; set-up dummy input data; multiply matrices using
the myMult() function above; average repeated runs. */
int main(int argc, char *argv[])
{
if(argc != 4)
{
fprintf(stderr,"Use: %s size nThreads nIter\n",argv[0]);
return -1;
}
int i,j,nt;
int size=atoi(argv[1]);
int nThreads=atoi(argv[2]);
int nIter=atoi(argv[3]);
omp_set_num_threads(nThreads);
/* when compiled in "mic-offload" mode, this memory gets allocated on host,
when compiled in "mic-native" mode, it gets allocated on mic. */
float (*restrict A)[size] = malloc(sizeof(float)*size*size);
float (*restrict B)[size] = malloc(sizeof(float)*size*size);
float (*restrict C)[size] = malloc(sizeof(float)*size*size);
/* this first pragma is just to get the actual #threads used
(sanity check). */
#pragma omp parallel
{
nt = omp_get_num_threads();
/* Fill the A and B arrays with dummy test data. */
#pragma omp parallel for default(none) shared(A,B,size) private(i,j)
for(i = 0; i < size; ++i)
{
for(j = 0; j < size; ++j)
{
A[i][j] = (float)i + j;
B[i][j] = (float)i - j;
}
}
}
/* warm up run to overcome setup overhead in benchmark runs below. */
myMult(size, A,B,C);
double aveTime,minTime=1e6,maxTime=0.;
/* run the matrix multiplication function nIter times and compute
average runtime. */
for(i=0; i < nIter; i++)
{
double startTime = dsecnd();
myMult(size, A,B,C);
double endTime = dsecnd();
double runtime = endTime-startTime;
maxTime=(maxTime > runtime)?maxTime:runtime;
minTime=(minTime < runtime)?minTime:runtime;
aveTime += runtime;
}
aveTime /= nIter;
printf("%s nThreads %d matrix %d maxRT %g minRT %g aveRT %g GFlop/s %g\n",
argv[0],nt,size,maxTime,minTime,aveTime, 2e-9*size*size*size/aveTime);
free(A);
free(B);
free(C);
return 0;
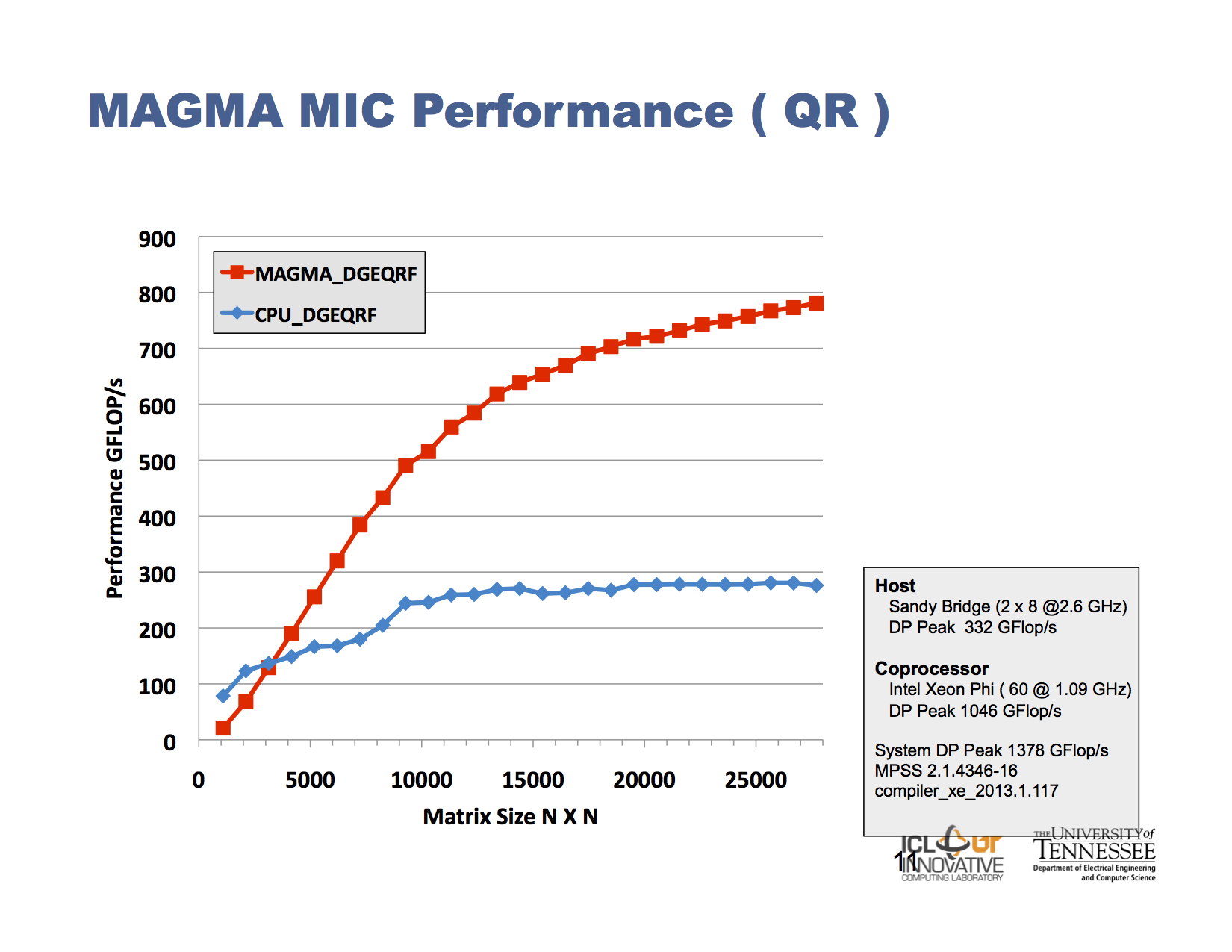
}I found an interesting talk by Hatem Ltaief about performance of BLAS (MAGA library) on Xeon Phi. Here is a slide from his talk.
Specs, Mother-board, Air-supply, …
There is a lot of info about the mother-board support and heat dissipation on forums. For example see this thread. I have a 5110P which is passively cooled. The specs of which from the Intel page is below
| L2 Cache | 30 MB |
| # of Cores | 60 |
| Processor Base Frequency | 1.053 GHz |
| Max Memory Size | 8 GB |
| Max Memory Bandwidth | 320 GB/s |

The card also requires sufficient air supply to make things work!. Puget-Systems has a case in which they have 3-D printed an air duct for Xeon Phi! From the thread, I decided to go for the specification suggested by Zibi Holka. Here are the specs
- ASUS GRYPHON (TUF) Z97 mATX motherboard! BIOS:2205 -standard BIOS
- Intel Core i7 i7-4790K CPU (Quad Core 4GHz, Socket H3 LGA-1150)
- Corsair Platinum 16GB 2x8GB Memory Kit (CMD32GX3M4A2133C9)
- Xeon PHI 31s1p
- Fedora 21
- Kernel (std. fedora): 3.18.7
- MPSS: 3.4.2 MPSS-Modules recompiled from https://github.com/xdsopl/mpss-modules
I may not get the exact CPU/Memory config and I have a 5110P instead of 31S1P. So far I have the first 4 in the list. I will update this blog as I make progress :)